6.4.4 Logarithmus
In Abschnitt 6.4.3 Eulersche Funktion haben wir beim Studium der -Funktion,
insbesondere auf eine sehr wichtige Eigenschaft der natürlichen Exponentialfunktion hingewiesen, nämlich dass diese Funktion streng monoton wachsend ist. Spiegelt man den Graph der Funktion an der Winkelhalbierenden zwischen dem ersten und dritten Quadranten (vgl. Modul 9 Orientierung im zweidimensionalen Koordinatensystem), so erhält man den Graphen der natürlichen Logarithmusfunktion - und versieht sie mit einem eigenen Symbol, nämlich :
Info 6.4.7
Die über die Gleichung erklärte Funktion
heißt die natürliche Logarithmusfunktion.
Die Gleichung ist dabei so zu lesen, dass derjenige Wert ist mit . Diese Konstruktion wird im folgenden Bild dargestellt:
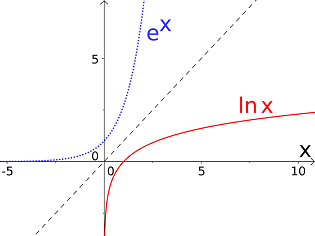
Folgende Eigenschaften der natürlichen Logarithmusfunktion können wir dem Graphen entnehmen:
- Die Funktion ist streng monoton wachsend.
- Nähert man sich von rechts auf der -Achse dem Nullpunkt, so nimmt immer größere negative Werte an: Wir halten fest, dass sich der Graph von an die negative -Achse anschmiegt.
- An der Stelle besitzt die natürliche Logarithmusfunktion den Wert , .
Neben der natürlichen Logarithmusfunktion gibt es noch andere Logarithmusfunktionen, die jeweils zu einem bestimmten Exponenten gehören:
Info 6.4.8
Ist ein beliebiger Exponent, so nennt man die über die Gleichung (sprich: ist derjenige Exponent mit ) erklärte Funktion
die allgemeine Logarithmusfunktion zur Basis .
Die Logarithmusfunktion kann man in der Regel nicht direkt ausrechnen. Da sie als die Umkehrfunktion zur Exponentialfunktion definiert ist, versucht man in der Regel, ihre Eingabe als Potenz zu schreiben und den Exponenten abzulesen.
Beispiel 6.4.9
Typische Berechnungen für den natürlichen Logarithmus sind
sowie für den allgemeinen Logarithmus
Dabei muss man auf die Basis des Logarithmus achten, beispielsweise ist
Aufgabe 6.4.10
Berechnen Sie diese Logarithmen:
- .
- .
- .
In der Mathematik und den Naturwissenschaften werden folgende Logarithmen häufig eingesetzt und erhalten deshalb besondere Symbole:
- Logarithmus zur Basis : oder manchmal auch nur , dieser Logarithmus gehört zu den Zehnerpotenzen und wird beispielsweise zur Berechnung von pH-Werten in der Chemie eingesetzt.
- Logarithmus zur Basis : , dieser Logarithmus ist in der Informatik wichtig.
- Logarithmus zur Basis : , der natürliche Logarithmus ist für praktische Rechnungen meist ungeeignet (es sei denn, der Ausdruck ist eine -Potenz). Er wird als natürlich bezeichnet, weil die Exponentialfunktion zur Basis aus mathematischer Sicht einfacher ist als die allgemeinen Exponentialfunktionen (z.B. weil seine eigene Ableitung ist, aber nicht, falls ).
Für die Logarithmusfunktion gibt es zahlreiche Rechenregeln, die im folgenden Abschnitt erklärt werden.