6.4.3 Eulersche Funktion
Es gibt eine ganz besondere Exponentialfunktion, manchmal auch als die Exponentialfunktion bezeichnet, um die wir uns jetzt kümmern wollen. In der Tat lassen sich, wie wir sehen werden, alle anderen Exponentialfunktionen auf diese besondere Exponentialfunktion zurückführen. Sie besitzt als Basis die eulersche Zahl . Ihr (ungefährer) Wert beträgt
Betrachten wir also - zunächst ohne irgendwelche zusätzlichen Parameter - den Graphen der Exponentialfunktion,
wegen der Basis auch -Funktion oder natürliche Exponentialfunktion genannt:
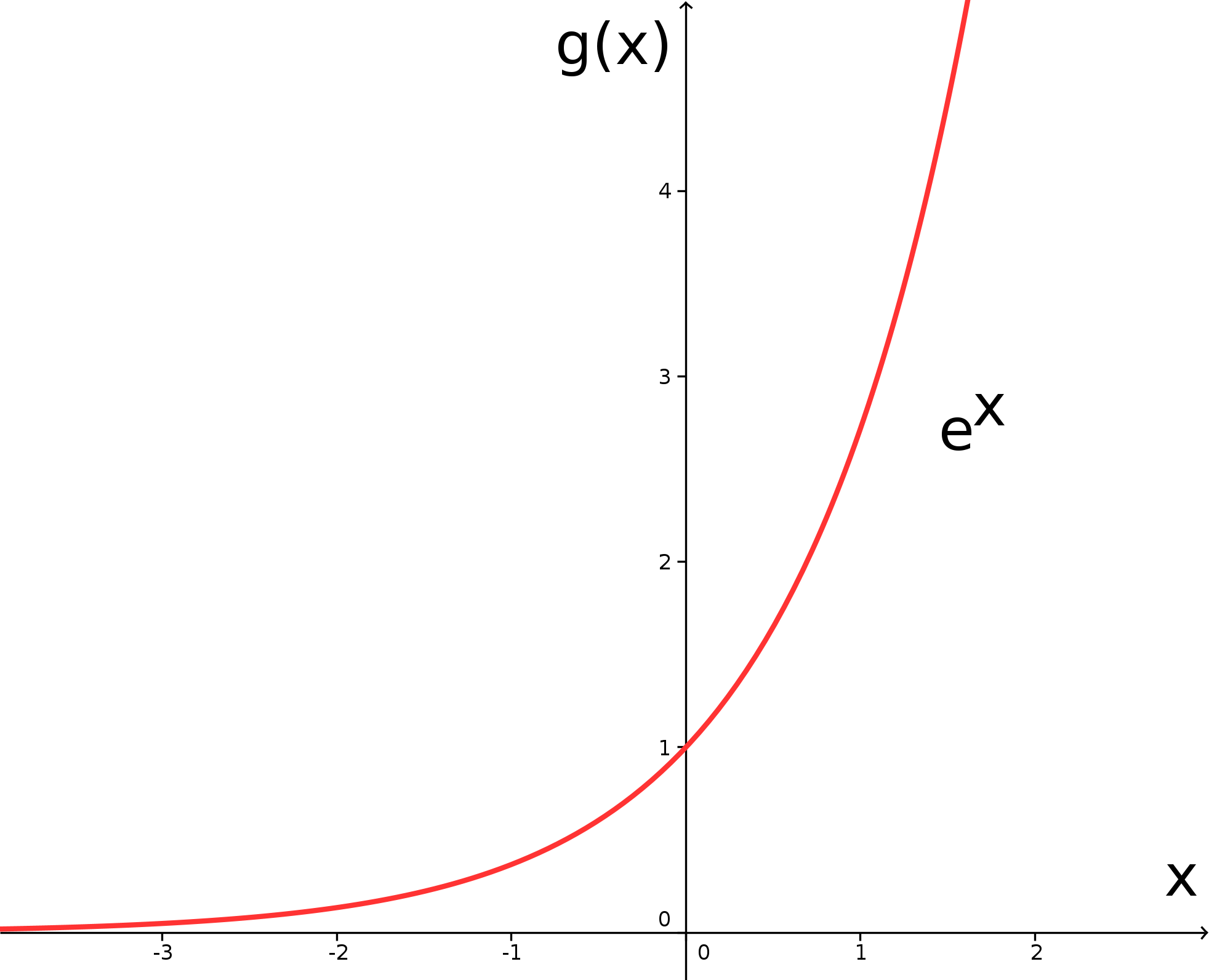
Wenig überraschend zeigt auch die -Funktion das bereits in 6.4.2 Inhalt diskutierte Verhalten der Exponentialfunktionen ; schließlich haben wir für die Basis ja auch nur einen speziellen Wert, nämlich , gewählt. Insbesondere halten wir nochmals fest, dass die -Funktion streng monoton wachsend ist, sich für große negative -Werte an die negative -Achse anschmiegt und für den Wert annimmt.
Aufgabe 6.4.4
Wie sieht der Graph der Funktion , aus, und welche generellen Eigenschaften besitzt diese Funktion?
Lösung
 | Die Funktion ist streng monoton fallend, für große positive -Werte schmiegt sich der Graph von an die | |
| positive -Achse an und für nimmt den Wert an. |
Eingangs dieses Unterabschnitts haben wir behauptet, dass sich die weiter oben besprochenen Exponentialfunktionen auf die -Funktion zurückführen lassen. Dies gelingt mit Hilfe der Identität
die für beliebige reelle und beliebige reelle gilt. Dabei bezeichnet den natürlichen Logarithmus, dessen Funktionsgestalt uns im folgenden Abschnitt 6.4.4 Logarithmus noch ausgiebig beschäftigen wird.
Aufgabe 6.4.5
Begründen Sie die Identität .
Allgemeine -Funktionen enthalten die bereits in Unterabschnitt 6.4.2 Inhalt eingeführten Parameter und ; ihre funktionale Gestalt sieht also folgendermaßen aus:
Wiederum repräsentiert die Möglichkeit von verschiedener Start- oder Anfangswerte, und der Faktor im Exponenten gestattet unterschiedlich starke (positive oder negative) Wachstumsraten. Wir wollen dies abschließend an einem Beispiel verdeutlichen:
Beispiel 6.4.6
Bei einer Versuchsreihe mit radioaktiven Jodatomen () ergeben sich im Mittel folgende Daten:
| Anzahl Jodatome | 10 000 | 5 000 | 2 500 | 1 250 | usw. |
|---|---|---|---|---|---|
| Anzahl Tage seit Beginn | 0 | usw. |
Mit anderen Worten: Alle Tage halbiert sich die Anzahl der Jodatome aufgrund radioaktiven Zerfalls; man spricht daher in diesem Zusammenhang davon, dass die Halbwertszeit von Jod- Tage beträgt.
Der radioaktive Zerfall folgt einem Exponentialgesetz:
Unsere Exponentialfunktion heißt hier ; sie gibt die Anzahl der noch vorhandenen Jodatome an. steht dementsprechend für die Anzahl der Jodatome zu Beginn, also . Die Veränderliche im vorliegenden Beispiel ist die Zeit (gemessen in Tagen). Von dem Parameter erwarten wir, dass er negativ ist, da es um die Beschreibung eines Zerfallsprozesses, also eines Prozesses mit negativem Wachstum, geht. Wir wollen in der Folge aus den Messdaten bestimmen:
Nach Tagen sind nur noch Jodatome vorhanden, d.h. . Verwenden wir das Exponentialgesetz für den radioaktiven Zerfall, so erhalten wir:
Wir können auf beiden Seiten der Gleichung kürzen und anschließend logarithmieren (siehe Abschnitt 6.4.4 Logarithmus):
Die linke Seite formen wir gemäß den Rechenregeln für den Logarithmus um (siehe Abschnitt 6.4.4 Logarithmus), . Für die rechte Seite beachten wir, dass Logarithmieren die Umkehrung zum Exponentieren darstellt, ; damit folgt:
Mit Tage für Jod- folgt für den Parameter im vorliegenden Fall
Andere radioaktive Substanzen besitzen andere Halbwertszeiten - Plutonium-239 z.B. weist eine Halbwertszeit von ungefähr Jahren auf - und führen folglich auf andere Werte für den Parameter im Exponentialgesetz für den radioaktiven Zerfall.