11.1.2 Rundung
Das Runden von Messergebnissen ist ein alltäglicher Vorgang.
Info 11.1.3
Für Rundungsvorgänge gibt es prinzipiell drei Möglichkeiten:
- Das (Ab)Runden mit Hilfe der -Funktion ,
- das (Auf)Runden mit Hilfe der -Funktion ,
- das Runden mit Hilfe der -Funktion, manchmal auch als -Funktion bezeichnet.
Die -Funktion (engl. floor = Fußboden, Diele) ist definiert durch
Ist eine reelle Zahl, so ist die größte ganze Zahl, die kleiner oder gleich x ist. Sie entsteht durch Abrundung von . Schreibt man eine positive reelle Zahl als Dezimalbruch, so ist die ganze Zahl vor dem Dezimalkomma: Die Abrundung schneidet die Nachkommastellen ab. Beispielsweise ist , aber . Die Floor-Funktion ist eine Treppenfunktion mit Sprungstellen in allen Punkten der Sprunghöhe . Die Funktionswerte in den Sprungstellen liegen immer oben. Dies ist in dem folgenden Schaubild des Graphen angedeutet durch eingezeichnete Punkte:
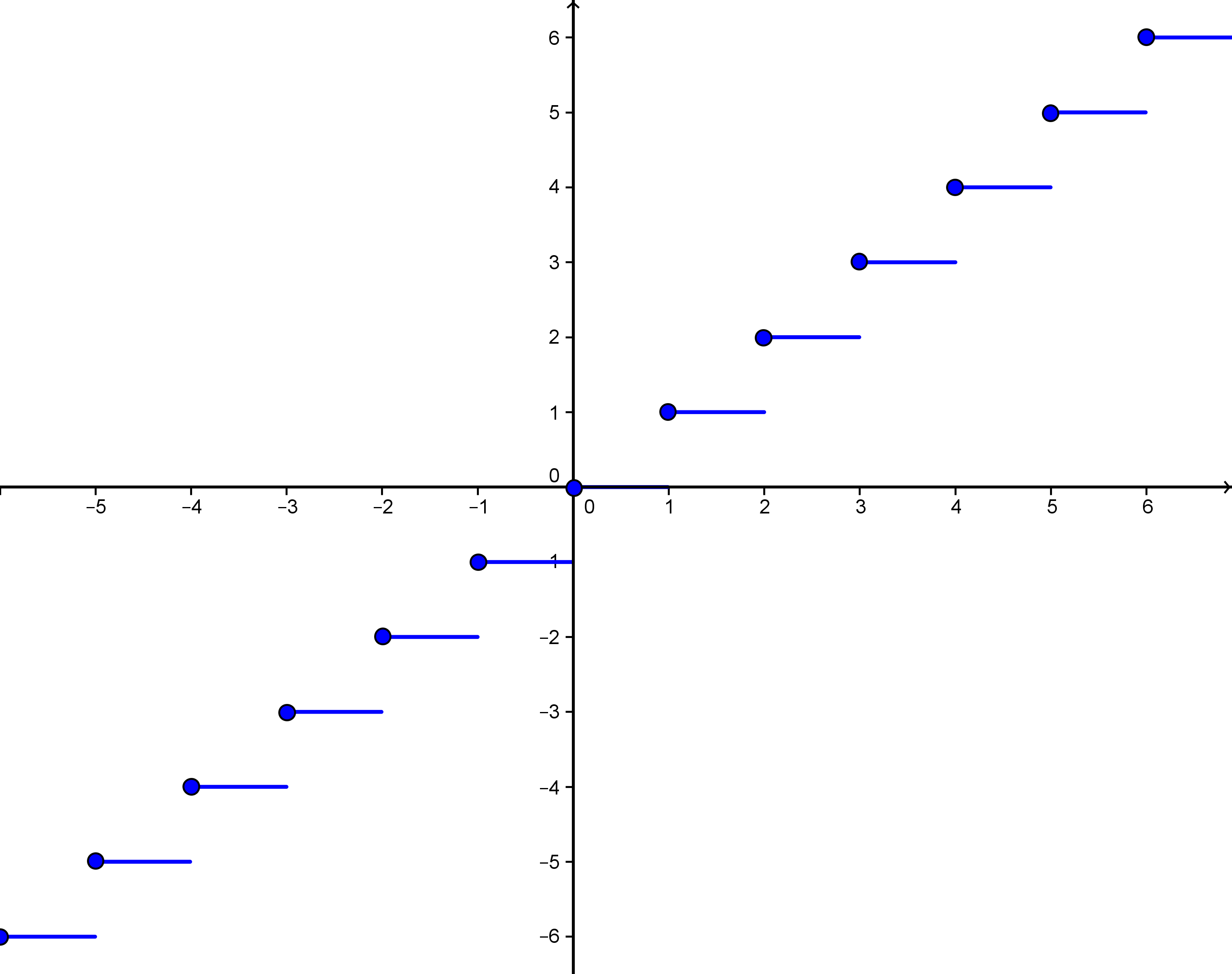Graph der -Funktion.Gegeben sei eine reelle Zahl , dargestellt als Dezimalbruch mit den Ziffern
Will man mit Hilfe der -Funktion die Zahl auf Stellen () nach dem Komma runden, so bildet man
Dieser Rundungsvorgang ist die Rundung durch Abschneiden nach der r-ten Nachkommastelle. Beim Rundungsverfahren mit Hilfe der -Funktion wird also grundsätzlich abgerundet.
Beispiel 11.1.4
wird mit Hilfe der -Funktion gerundet auf 2 Nachkommastellen zu
oder einfach durch Abschneiden aller Nachkommastellen nach der zweiten Stelle (das geht aber nur, wenn die Zahl schon als Dezimalbruch vorliegt, was beispielsweise in einem Computerprogramm oft nicht der Fall ist). Die Zahl wird mit Hilfe der -Funktion auf 4 Nachkommastellen zu
gerundet. Die Kreiszahl
wird mit Hilfe der -Funktion gerundet auf 2 Stellen nach dem Komma zu
Das Rundungsverfahren mit Hilfe der -Funktion findet oft Anwendung bei der Bestimmung von Gesamtnoten in Zeugnissen („akademische Rundung"). Hat ein Studierender im Fach Mathematik z.B. die Einzelnoten
| Fach | Note |
|---|---|
| Mathematik 1 | |
| Mathematik 2 | |
| Mathematik 3 |
so wird das arithmetische Mittel dieser drei Noten
gebildet. Die Rundung mit Hilfe der -Funktion auf eine Nachkommastelle würde die Gesamtnote Mathematik ergeben. Die zur Bildung von Gesamtnoten verwendeten Rundungsverfahren müssen in den jeweiligen Prüfungsordnungen stets genau beschrieben sein. Das Gegenstück zur -Funktion ist die -Funktion:
Info 11.1.5
Die -Funktion (engl. ceil = Zimmerdecke, Decke) ist definiert durch
Ist eine reelle Zahl, so ist die kleinste ganze Zahl, die größer oder gleich ist. Die -Funktion ist eine Treppenfunktion mit Sprungstellen in allen Punkten der Sprunghöhe . Die Funktionswerte in den Sprungstellen liegen immer unten. Dies ist in dem folgenden Schaubild des Graphen der -Funktion angedeutet durch eingezeichnete Punkte:
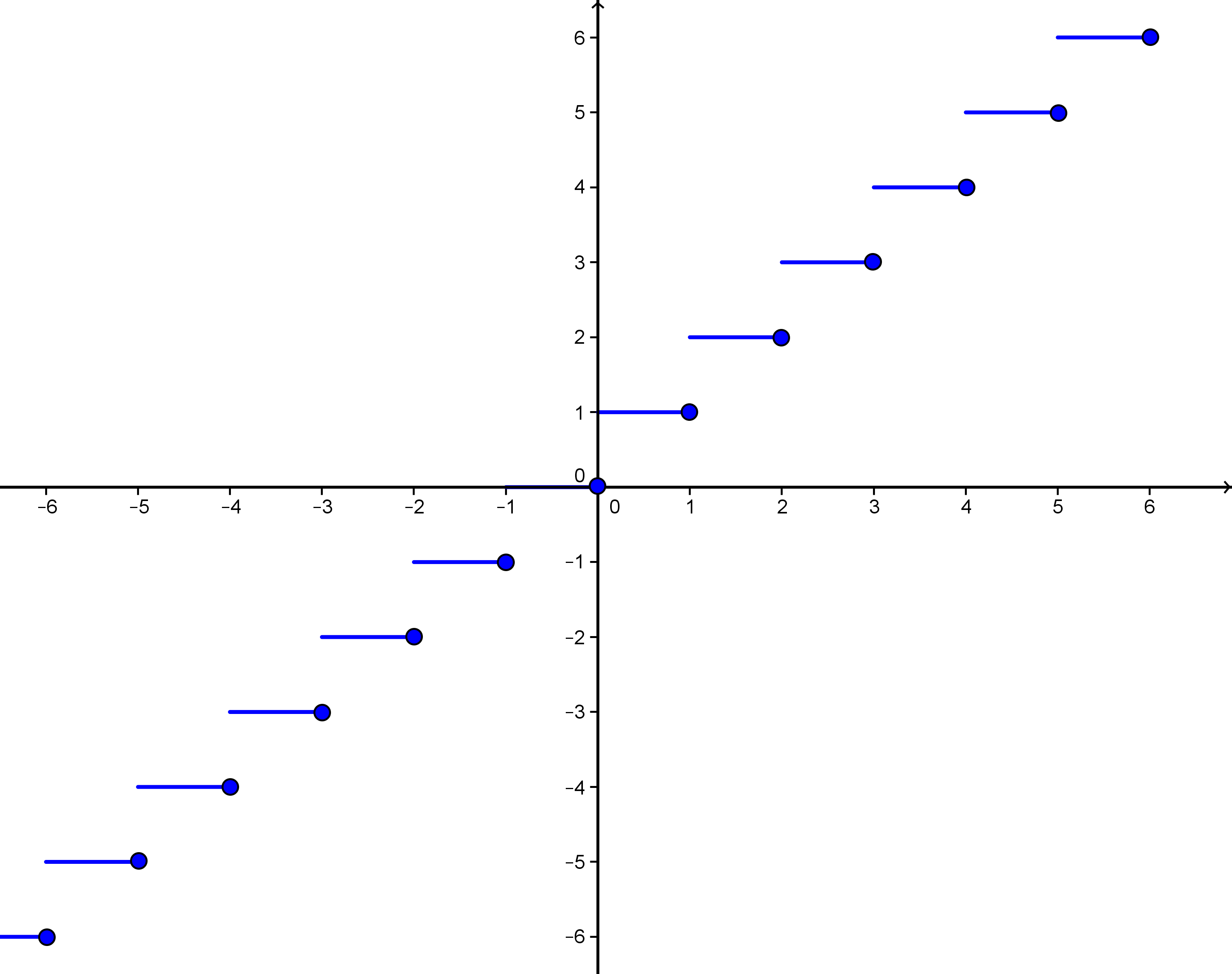Graph der -Funktion.Gegeben sei eine reelle Zahl , dargestellt als Dezimalbruch mit den Ziffern
Will man mit Hilfe der -Funktion die Zahl auf Stellen () nach dem Komma runden, so bildet man
Bei diesem Rundungsvorgang wird stets aufgerundet auf die nächsthöhere Dezimalstelle.
Beispiel 11.1.6
Die Zahl wird mit Hilfe der -Funktion gerundet auf Nachkommastellen zu
Analog wird mit Hilfe der -Funktion auf Nachkommastellen zu
gerundet. Die Kreiszahl wird mit Hilfe der -Funktion gerundet auf Stellen nach dem Komma zu
Rundungsverfahren mit Hilfe der -Funktion findet man z.B. häufig bei Handwerkerrechnungen. Ein Handwerker wird meistens nach Arbeitsstunden bezahlt. Dauert eine Reparatur 50 Minuten (das sind Stunden im Dezimalsystem), so wird trotzdem aufgerundet und eine volle Arbeitsstunde berechnet. Spricht man umgangssprachlich von Runden, so ist meist die mathematische Rundung gemeint:
Info 11.1.7
Die -Funktion (oder mathematische Rundung) ist definiert durch
Im Gegensatz zur Auf- und Abrundung beträgt die durch diese Rundung an der Zahl vorgenommene Veränderung höchstens .
Die -Funktion ist eine Treppenfunktion mit Sprungstellen in allen Punkten , der Sprunghöhe . Die Funktionswerte in den Sprungstellen liegen immer oben. Dies ist in dem folgenden Schaubild des Graphen der -Funktion angedeutet durch eingezeichnete Punkte:
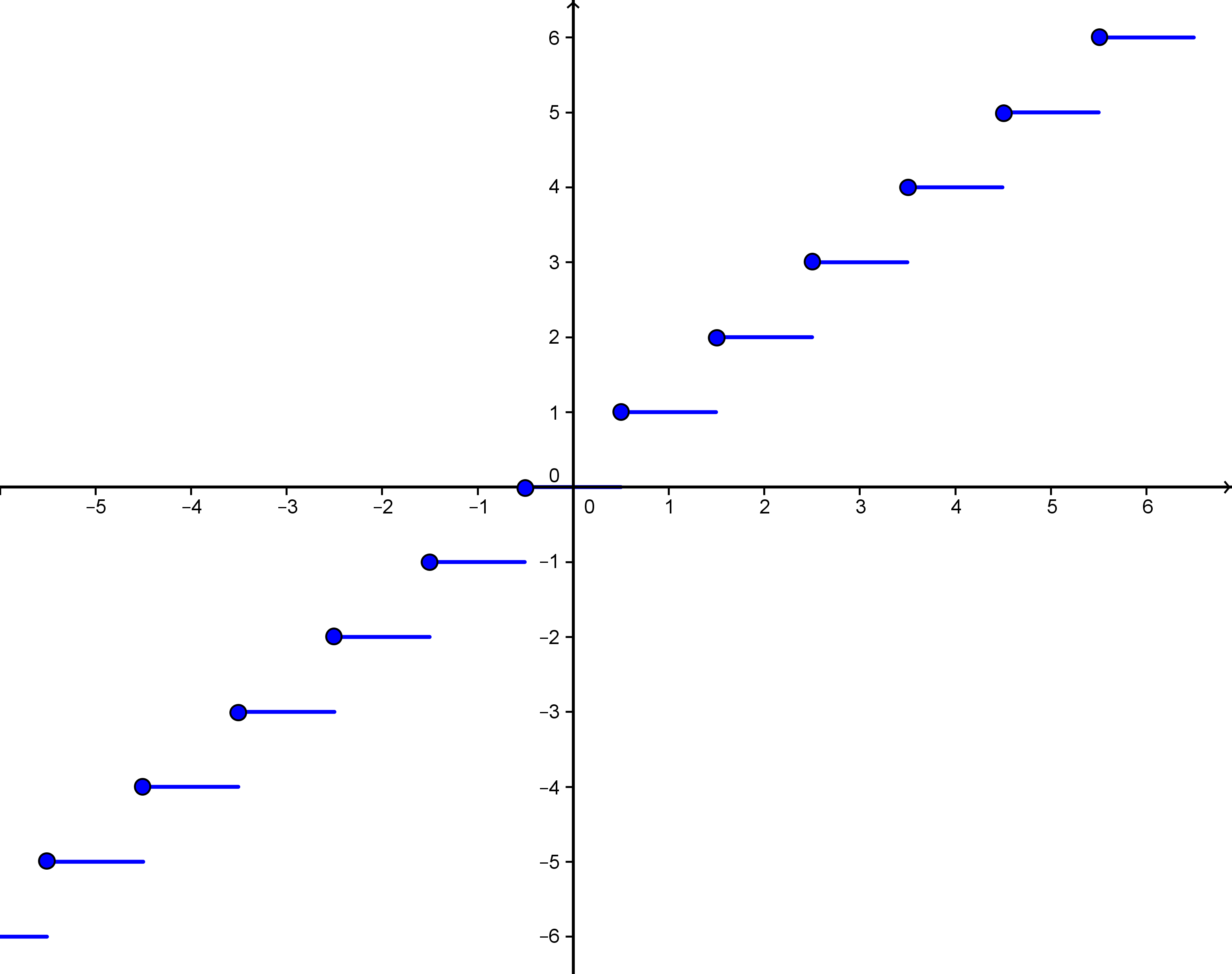Graph der -Funktion.Gegeben sei eine reelle Zahl , dargestellt als Dezimalbruch mit den Ziffern
Will man mit Hilfe der Round-Funktion die Zahl auf () Stellen nach dem Komma runden, so bildet man
Dieser Rundungsvorgang entspricht dem üblichen sogenannten mathematischen Runden.
Beispiel 11.1.8
Die Zahl wird mit Hilfe der -Funktion auf eine Nachkommestelle gerundet zu
Die Zahl wird mit Hilfe der -Funktion auf eine Nachkommestelle gerundet zu
Die Zahl wird mit Hilfe der -Funktion gerundet auf Nachkommastellen zu
Die Zahl wird mit Hilfe der -Funktion gerundet auf Nachkommastellen zu
Aufgabe 11.1.9
Berechnen Sie mit Hilfe der -Funktion die Rundung von auf Nachkommastellen: .
Aufgabe 11.1.10
Vorgegeben seien die Zahlen
- Runden Sie die Zahlen und mit Hilfe der -Funktion auf jeweils Nachkommastellen: Die Rundungen ergeben sowie .
- Runden Sie die Zahlen und mit Hilfe der -Funktion auf jeweils Nachkommastellen: Die Rundungen ergeben sowie .
- Runden Sie die Zahlen und mit Hilfe der -Funktion auf jeweils Nachkommastellen: Die Rundungen ergeben sowie .